RICHARD DAWKINSTHE BLIND WATCHMAKER |
|
CHAPTER 3 ACCUMULATINGSMALL CHANGE
|
|
44 The Blind Watchmaker The waves and the pebbles together constitute a simple example of a system that automatically generates non-randomness. The world is full of such systems. The simplest example I can think of is a hole. Only objects smaller than the hole can pass through it. This means that if you start with a random collection of objects above the hole, and some force shakes and jostles them about at random, after a while the objects above and below the hole will come to be nonrandomly sorted. The space below the hole will tend to contain objects smaller than the hole, and the space above will tend to contain objects larger than the hole. Mankind has, of course, long exploited this simple principle for generating non-randomness, in the useful device known as the sieve. The Solar System is a stable arrangement of planets, comets and debris orbiting the sun, and it is presumably one of many such orbiting systems in the universe. The nearer a satellite is to its sun, the faster it has to travel if it is to counter the sun's gravity and remain in stable orbit. For any given orbit, there is only one speed at which a satellite can travel and remain in that orbit. If it were travelling at any other velocity, it would either move out into deep space, or crash into the Sun, or move into another orbit. And if we look at the planets of our solar system, lo and behold, every single one of them is travelling at exactly the right velocity to keep it in its stable orbit around the Sun. A blessed miracle of provident design? No, just another natural 'sieve'. Obviously all the planets that we see orbiting the sun must be travelling at exactly the right speed to keep them in their orbits, or we wouldn't see them there because they wouldn't be there! But equally obviously this is not evidence for conscious design. It is just another kind of sieve. Sieving of this order of simplicity is not, on its own, enough to account for the massive amounts of nonrandom order that we see in living things. Nowhere near enough. Remember the analogy of the combination lock. The kind of non-randomness that can be generated by simple sieving is roughly equivalent to opening a combination lock with only one dial: it is easy to open it by sheer luck. The kind of nonrandomness that we see in living systems, on the other hand, is equivalent to a gigantic combination lock with an almost uncountable number of dials. To generate a biological molecule like haemoglobin, the red pigment in blood, by simple sieving would be equivalent to taking all the amino-acid building blocks of haemoglobin, jumbling them up at random, and hoping that the haemoglobin molecule would reconstitute itself by sheer luck. The amount of luck that would be required for this feat is unthinkable, and has been used as a telling mind-boggier by Isaac Asimov and others.
|
|
Accumulating small change 45 A haemoglobin molecule consists of four chains of amino acids twisted together. Let us think about just one of these four chains. It consists of 146 amino acids. There are 20 different kinds of amino acids commonly found in living things. The number of possible ways of arranging 20 kinds of thing in chains 146 links long is an inconceivably large number, which Asimov calls the 'haemoglobin number'. It is easy to calculate, but impossible to visualize the answer. The first link in the 146-long chain could be any one of the 20 possible amino acids. The second link could also be any one of the 20, so the number of possible 2-link chains is 20 x 10, or 400. The number of possible 3-link chains is 20 x 20 x 20, or 8,000. The number of possible 146-link chains is 20 times itself 146 times. This is a staggeringly large number. A million is a 1 with 6 noughts after it. A billion 11,000 million) is a 1 with 9 noughts after it. The number we seek, the 'haemoglobin number', is (near enough) a 1 with 190 noughts after it! This is the chance against happening to hit upon haemoglobin by luck. And a haemoglobin molecule has only a minute fraction of the complexity of a living body. Simple sieving, on its own, is obviously nowhere near capable of generating the amount of order in a living thing. Sieving is an essential ingredient in the generation of living order, but it is very far from being the whole story. Something else is needed. To explain the point, I shall need to make a distinction between 'single-step' selection and 'cumulative' selection. The simple sieves we have been considering so far in this chapter are all examples of single-step selection. Living organization is the product of cumulative selection. The essential difference between single-step selection and cumulative selection is this. In single-step selection the entities selected or sorted, pebbles or whatever they are, are sorted once and for all. In cumulative selection, on the other hand, they 'reproduce'; or in some other way the results of one sieving process are fed into a subsequent sieving, which is fed into . . ., and so on. The entities are subjected to selection or sorting over many 'generations' in succession. The end-product of one generation of selection is the starting point for the next generation of selection, and so on for many generations. It is natural to borrow such words as 'reproduce' and 'generation', which have associations with living things, because living things are the main examples we know of things that participate in cumulative selection. They may in practice be the only things that do. But for the moment I don't want to beg that question by saying so outright. Sometimes clouds, through the random kneading and carving of the winds, come to look like familiar objects. There is a much published photograph, taken by the pilot of a small aeroplane, of what looks a bit
|
|
46 The Blind Watchmaker like the face of Jesus, staring out of the sky. We have all seen clouds that reminded us of something - a sea horse, say, or a smiling face. These resemblances come about by single-step selection, that is to say by a Single coincidence. They are, consequently, not very impressive. The resemblance of the signs of the zodiac to the animals after which they are named, Scorpio, Leo, and so on, is as unimpressive as the predictions of astrologers. We don't feel overwhelmed by the resemblance, as we are by biological adaptations - the products of cumulative selection. We describe as weird, uncanny or spectacular, the resemblance of, say, a leaf insect to a leaf or a praying mantis to a cluster of pink flowers. The resemblance of a cloud toaweaselisonly mildly diverting, barely worth calling to the attention of our companion. Moreover, we are quite likely to change our mind about exactly what the cloud most resembles. Hamlet. Do you see yonder cloud that's almost in shape of a camel? Polonius. By the mass, and 'tis like a camel, indeed. Hamlet. Methinks it is like a weasel. Polonius. It is backed like a weasel. Hamlet. Or like a whale? Polonius. Very like a whale. I don't know who it was first pointed out that, given enough time, a monkey bashing away at random on a typewriter could produce all the works of Shakespeare. The operative phrase is, of course, given enough time. Let us limit the task facing our monkey somewhat. Suppose that he has to produce, not the complete works of Shakespeare but just the short sentence 'Methinks it is like a weasel', and we shall make it relatively easy by giving him a typewriter with a restricted keyboard, one with just the 26 (capital) letters, and a space bar. How long will he take to write this one little sentence? The sentence has 28 characters in it, so let us assume that the monkey has a series of discrete 'tries', each consisting of 28 bashes at the keyboard. If he types the phrase correctly, that is the end of the experiment. If not, we allow him another 'try' of 28 characters. I don't know any monkeys, but fortunately my 11-month old daughter is an experienced randomizing device, and she proved only too eager to step into the role of monkey typist. Here is what she typed on the computer: UMMK JK CDZZ F ZD DSDSKSM S SS FMCV PU I DDRGLKDXRRDO RDTE QDWFDVIOY UDSKZWDCCVYT H CHVY NMGNBAYTDFCCVD D RCDFYYYRM N DFSKD LD K WDWK HKAUIZMZI UXDKIDISFUMDKUDXI
|
|
|
|
|
|
Accumulating small change 47 She has other important calls on her time, so I was obliged to program the computer to simulate a randomly typing baby or monkey: WDLDMNLT DTJBKWIRZREZLMQCO P Y YVMQKZPGJXWVHGLAWFVCHQYOPY MWR SWTNUXMLCDLEUBXTQHNZVIQF FU OVAODVYKDGXDEKYVMOGGS VT HZQZDSFZIHIVPHZPETPWVOVPMZGF GEWRGZRPBCTPGQMCKHFDBGW ZCCF And so on and on. It isn't difficult to
calculate how long we should reasonably'expect to
wait for the random computer (or baby or So much for single-step selection of random variation. What about cumulative selection; how much more effective should this be? Very very much more effective, perhaps more so than we at first realize, although it is almost obvious when we reflect further. We again use our computer monkey, but with a crucial difference in its program. It again begins by choosing a random sequence of 28 letters, just as before: WDLMNLT DTJBKWIRZREZLMQCO P It now 'breeds from' this random phrase. It duplicates it repeatedly, but with a certain chance of random error - 'mutation' - in the copying. The computer examines the mutant nonsense phrases, the 'progeny' of the original phrase, and chooses the one which, however slightly, most resembles the target phrase, METHINKS IT IS LIKE A
|
|
|
|
|
|
48 The Blind Watchmaker WEASEL. In this instance the winning phrase of the next 'generation' happened to be: WDLTMNLT DTJBSWIRZREZLMQCO P Not an obvious improvement! But the procedure is repeated, again mutant 'progeny' are 'bred from' the phrase, and a new 'winner' is chosen. This goes on, generation after generation. After 10 generations, the phrase chosen for 'breeding' was: MDLDMNLS ITpSWHRZREZ MECS P After 20 generations it was: MELDINLS IT ISWPRKE Z WECSEL By now, the eye of faith fancies that it can see a resemblance to the target phrase. By 30 generations there can be no doubt: METHINGS IT ISWLIKE B WECSEL Generation 40 takes us to within one letter of the target: METHINKS IT IS LIKE I WEASEL And the target was finally reached in generation 43. A second run of the computer began with the phrase: Y YVMQKZPFfXWVHGLAWFVCHQXYOPY, passed through (again reporting only every tenth generation): Y YVMQKSPFTXWSHLIKEFV HQYSPY YETHINKSPITXISHLIKEFA WQYSEY METHINKS IT ISSLIKE A WEFSEY METHINKS IT ISBLIKE A WEASES METHINKS IT ISJLIKE A WEASEO METHINKS IT IS LIKE A WEASEP and reached the target phrase in generation 64. m a third run the computer started with: GEWRGZRPBCTPGQMCKHFDBGW ZCCF and reached METHINKS IT IS LIKE A WEASEL in 41 generations of selective 'breeding'. The exact time taken by the computer to reach the target doesn't matter. If you want to know, it completed the whole exercise for me, the first time, while I was out to lunch. It took about half an hour. (Computer enthusiasts may think this unduly slow. The reason is that
|
|
|
|
|
|
Accumulating small change 49 the program was written in BASIC, a sort of
computer baby-talk. When I rewrote it in Pascal, it took 11 seconds.)
Computers are a bit faster at this kind of thing than monkeys, but the
difference really isn't significant. What matters is the difference between
the time taken by cumulative
selection, and the time
which the same computer, There is a big difference, then, between cumulative selection (in which each improvement, however slight, is used as a basis for future building), and single-step selection (in which each new 'try' is a fresh one). If evolutionary progress had had to rely on single-step selection, it would never have got anywhere. If, however, there was any way in which the necessary conditions for cumulative selection could have been set up by the blind forces of nature, strange and wonderful might have been the consequences. As a matter of fact that is exactly what happened on this planet, and we ourselves are among the most recent, if not the strangest and most wonderful, of those consequences. It is amazing that you can still read
calculations like my haemoglobin calculation, used
as though they constituted arguments against
Clouds are not capable of entering into cumulative selection. There is no mechanism whereby clouds of particular shapes can spawn daughter clouds resembling themselves. If there were such a mechanism, if a cloud resembling a weasel or a camel could give rise to
|
|
50 The Blind Watchmaker a lineage of othel
clouds of roughly the same shape, cumulative selection would have the
opportunity to get going. Of course, clouds do break up and form 'daughter'
clouds sometimes, but this isn't enough for cumulative selection. It is also
necessary that the 'progeny' of any given cloud should resemble its 'parent' more than it resembles any old 'parent' in the 'population'. This
vitally important point is apparently misunderstood by some of the
philosophers who have, in recent years, taken an interest in the theory of
natural selection. It is further Although the monkey/Shakespeare model is useful for explaining the distinction between single-step selection and cumulative selection, it is misleading in important ways. One of these is that, in each generation of selective 'breeding', the mutant 'progeny' phrases were judged according to the criterion of resemblance to a distant ideal target, the phrase METHINKS IT IS LIKE A WEASEL. Life isn't like that. Evolution has no long-term goal. There is no long-distance target, no final perfection to serve as a criterion for selection, although human vanity cherishes the absurd notion that our species is the final goal of evolution. In real life, the criterion for selection is always short-term, either simple survival or, more generally, reproductive success. If, after the aeons, what looks like progress towards some distant goal seems, with hindsight, to have been achieved, this is always an incidental consequence of many generations of short-term selection. The 'watchmaker' that is cumulative natural selection is blind to the future and has no long-term goal. We can change our computer model to take account of this point. We can also make it more realistic in other respects. Letters and words are peculiarly human manifestations, so let's make the computer draw pictures instead. Maybe we shall even see animal-like shapes evolving in the computer, by cumulative selection of mutant forms. We shan't prejudge the issue by building-in specific animal pictures to start with. We want them to emerge solely as a result of cumulative selection of random mutations. In real life, the form of each individual animal is produced by embryonic development. Evolution occurs because, in successive generations, there are slight differences in embryonic development.
|
|
Accumulating small change 51 These
differences come about because of changes (mutations - this is the small
random element in the process that I spoke of) in the genes controlling
development. In our computer model, therefore, we must have something
equivalent to embryonic development, and something equivalent to genes that
can mutate. There are many ways in which we could meet these specifications
in a computer model. I chose one and wrote a program that embodied it. I
shall now describe this computer model, because I think it is revealing. If
you don't know anything about computers, just remember that they are machines
that do exactly what you tell them but often surprise you in the result. A
list of instructions for a computer is called a program (this is standard
American spelling, and it is also recommended by the Oxford Dictionary: the
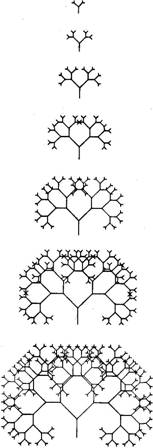
alternative, 'programme', commonly used in Embryonic development is far too elaborate a process to simulate realistically on a small computer. We must represent it by some simplified analogue. We must find a simple picture-drawing rule that the computer can easily obey, and which can then be made to vary under the influence of 'genes'. What drawing rule shall we choose? Textbooks of computer science often illustrate the power of what they call 'recursive' programming with a simple tree-growing procedure. The computer starts by drawing a single vertical line. Then the line branches into two. Then each of the branches splits into two subbranches. Then each of the sub-branches splits into sub-sub-branches, and so on. It is 'recursive' because the same rule (in this case a branching rule) is applied locally all over the growing tree. No matter how big the tree may grow, the same branching rule goes on being applied at the tips of all its twigs. The 'depth' of recursion, means the number of sub-sub-. .. branches that are allowed to grow, before the process is brought to a halt. Figure 2 shows what happens when you tell the computer to obey exactly the same drawing rule, but going on to various depths of recursion. At high levels of recursion the pattern becomes quite elaborate, but you can easily see in Figure 2 that it is still produced by the same very simple branching rule. This is, of course, just what happens in a real tree. The branching pattern of an oak tree or an apple free looks complex, but it really isn't. The basic branching rule is very simple. It is because it is applied recursively at the growing tips all over the tree - branches make sub-branches, then each sub-branch makes sub-sub-branches, and so on - that the whole tree ends up large and bushy. Recursive branching is also a good metaphor for the embryonic development of plants and animals generally. I don't mean that animal
|
|
52 The Blind Watchmaker
|
|
|
|
Figure 2 embryos look like branching trees. They don't. But all embryos grow by cell division. Cells always split into two daughter cells. And genes always exert their final effects on bodies by means of local influences on cells, and on the two-way branching patterns of cell division. An animal's genes are never a grand design, a blueprint for the whole body. The genes, as we shall see, are more like a recipe than like a blueprint; and a recipe, moreover, that is obeyed not by the developing embryo as
|
|
Accumulating small change 53 a whole, but by each cell or each local cluster of dividing cells. I'm not denying that the embryo, and later the adult, has a large-scale form. But this large-scale form emerges because of lots of little local cellular effects all over the developing body, and these local effects consist primarily of two-way branchings, in the form of two-way cell splittings. It is by influencing these local events that genes ultimately exert influences on the adult body. The simple branching rule for drawing trees, then, looks like a promising analogue for embryonic development. Accordingly, we wrap it up in a little computer procedure, label it DEVELOPMENT, and prepare to embed it in a larger program labelled EVOLUTION. As a first step towards writing this larger program, we now turn our attention to genes. How shall we represent 'genes' in our computer model? Genes in real life do two things. They influence development, and they get passed on to future generations. In real animals and plants there are tens of thousands of genes, but we shall modestly limit our computer model to nine. Each of the nine genes is simply represented by a number in the computer, which will be called its value. The value of a particular gene might be, say 4, or -7. How shall we make these genes influence
development? There are lots of things they could do. The basic idea is that
they should exert some minor quantitative influence on the drawing rule that
is DEVELOPMENT. For instance, one gene might influence the angle of branching, another might influence the length of some
particular branch. Another obvious thing for a gene to do is to influence the
depth of the recursion, the number of successive branchings.
I made Gene 9 have this effect. You can regard Figure 2, therefore, as a
picture of seven related organisms, identical to each other except with
respect to Gene
|
|
54 The Blind Watchmaker
|
|
|
|
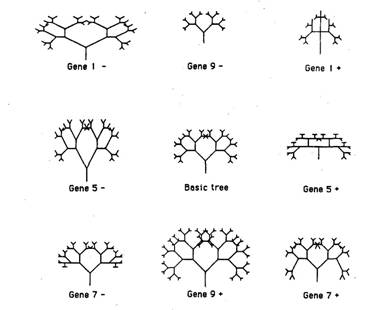
Figure 3 Each of these trees has its own, unique
'genetic formula', the numerical values of its nine genes. I haven't written
the genetic formulae down, because they wouldn't mean anything to you, in
themselves. That is true of real genes too. Genes only start to mean This, too, is exactly what real-life geneticists do. Geneticists normally don't know how genes exert their effects on embryos. Nor do they know the complete genetic formula of any animal. But by
|
|
Accumulating small change 55 comparing the bodies of two adult animals that are known to differ according to a single gene, they can see what effects that single gene has. It is more complicated than that, because the effects of genes interact with each other in ways that are more complicated than simple addition. Exactly the same is true of the computer trees. Very much so, as later pictures will show. You will notice that all the shapes are symmetrical about a left/right axis. This is a constraint that I imposed on the DEVELOPMENT procedure. I did it partly for aesthetic reasons; partly to economize on the number of genes necessary (if genes didn't exert mirror-image effects on the two sides of the tree, we'd need separate genes for the left and the right sides); and partly because I was hoping to evolve animal-like shapes, and most animal bodies are pretty symmetrical. For the same reason, from now on I shall stop calling these creatures 'trees', and shall call them 'bodies' or 'biomorphs'. Biomorph is the name coined by Desmond Morris for the vaguely animal-like shapes in his surrealist paintings. These paintings have a special place in my affections, because one of them was reproduced on the cover of my first book. Desmond Morris claims that his biomorphs 'evolve' in his mind, and that their evolution can be traced through successive paintings. Back to the computer biomorphs, and the ring of 18 possible mutants, of which a representative eight are drawn in Figure 3. Since each member of the ring is only one mutational step away from the central biomorph, it is easy for us to see them as children of the central parent. We have our analogue of REPRODUCTION, which, like DEVELOPMENT, we can wrap up in another small computer program, ready to embed in our big program called EVOLUTION. Note two things about REPRODUCTION. First, there is no sex; reproduction is asexual. I think of the biomorphs as female, therefore, because asexual animals like greenfly are nearly always basically female in form. Second, my mutations are all constrained to occur one at a time. A child differs from its parent at only one of the nine genes; moreover, all mutation occurs by +1 or — 1 being added to the value of the corresponding parental gene. These are just arbitrary conventions: they could have been different and still remained biologically realistic. The same is not true of the following feature of the model, which embodies a fundamental principle of biology. The shape of each child is not derived directly from the shape of the parent. Each child gets its shape from the values of its own nine genes (influencing angles, distances, and so on). And each child gets its nine genes from its parent's nine genes. This is just what happens in real life. Bodies don't get passed down the generations; genes do. Genes influence embryonic
|
|
56 The Blind Watchmaker development of the body in which they are sitting. Then those same genes either get passed on to the next generation or they don't. The nature of the genes is unaffected by their participation in bodily development, but their likelihood of being passed on may be affected by the success of the body that they helped to create. This is why, in the computer model, it is important that the two procedures called DEVELOPMENTandREPRODUCTIONarewrittenastwowatertight compartments. They are watertight except that REPRODUCTION passes gene values across to DEVELOPMENT, where they influence the growing rules. DEVELOPMENT most emphatically does not pass gene values back to REPRODUCTION - that would be tantamount to 'Lamarckism' (see Chapter 11). We have assembled our two program modules, then, labelled DEVELOPMENT and REPRODUCTION. REPRODUCTION passes genes down the generations, with the possibility of mutation. DEVELOPMENT takes the genes provided by REPRODUCTION in any given generation, and translates those genes into drawing action, and hence into a picture of a body on the computer screen. The time has come to bring the two modules together in the big program called EVOLUTION. EVOLUTION basically consists of endless repetition of REPRODUCTION. In every generation, REPRODUCTION takes the genes that are supplied to it by the previous generation, and hands them on to the next generation but with minor random errors - mutations. A mutation simply consists in +1 or — 1 being added to the value of a randomly chosen gene. This means that, as the generations go by, the total amount of genetic difference from the original ancestor can become very large, cumulatively, one small step at a time. But although the mutations are random, the cumulative change over the generations is not random. The progeny in any one generation are different from their parent in random directions. But which of those progeny is selected to go forward into the next generation is not random. This is where Darwinian selection comes in. The criterion for selection is not the genes themselves, but the bodies whose shape the genes influence through DEVELOPMENT. In addition to being REPRODUCED, the genes in each generation are also handed to DEVELOPMENT, which grows the appropriate body on the screen, following its own strictly laid-down rules. In every generation, a whole 'litter' of 'children' (i.e. individuals of the next generation) is displayed. All these children are mutant children of the same parent, differing from their parent with respect to one gene each. This very high mutation rate is a distinctly unbiological feature of the
|
|
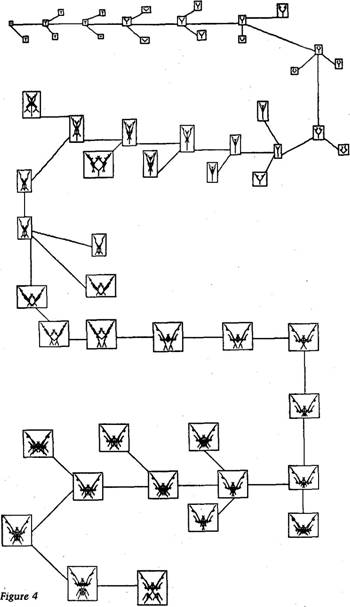
Accumulating small change 57 computer model. In real life, the probability that a gene will mutate is often less than one in a million. The reason for building a high mutation rate into the model is that the whole performance on the computer screen is for the benefit of human eyes, and humans haven't the patience to wait a million generations for a mutation! The human eye has an active role to play in the story. It is the selecting agent. It surveys the litter of progeny and chooses one for breeding. The chosen one then becomes the parent of the next generation, and a litter of its mutant children are displayed simultaneously on the screen. The human eye is here doing exactly what it does in the breeding of pedigree dogs or prize roses. Our model, in other words, is strictly a model of artificial selection, not natural selection. The criterion for 'success' is not the direct criterion of survival, as it is in true natural selection. In true natural selection, if a body has what it takes to survive, its genes automatically survive because they are inside it. So the genes that survive tend to be, automatically, those genes that confer on bodies the qualities that assist them to survive. In the computer model, on the other hand, the selection criterion is not survival, but the ability to appeal to human whim. Not necessarily idle, casual whim, for we can resolve to select consistently for some quality such as 'resemblance to a weeping willow'. In my experience, however, the human selector is more often capricious and opportunistic. This, too, is not unlike certain kinds of natural selection. The human tells the computer which one of the current litter of progeny to breed from. The genes of the chosen one are passed across to REPRODUCTION, and a new generation begins. This process, like real-life evolution, goes on indefinitely. Each generation of biomorphs is only a single mutational step away from its predecessor and its successor. But after 100 generations of EVOLUTION, the biomorphs can be anything up to 100 mutational steps away from their original ancestor. And in 100 mutational steps, much can happen. I never dreamed how much, when I first started to play with my newly written EVOLUTION program. The main thing that surprised me was that the biomorphs can pretty quickly cease to look like trees. The basic two-way branching structure is always there, but it is easily smothered as lines cross and recross one another, making solid masses of colour (only black and white in the printed pictures). Figure 4 shows one particular evolutionary history consisting of no more than 29 generations. The ancestor is a tiny creature, a single dot. Although the ancestor's body is a dot, like a bacterium in the primeval slime, hidden inside'it is the potential for branching in exactly the pattern of the
|
|
|
|
The Blind Watchmaker
|
|
|
|
Accumulating small change 59 central tree of Figure 3: it is just that its Gene 9 tells it to branch zero times! All the creatures pictured on the page are descended from the dot but, in order to avoid cluttering the page, I haven't printed all the descendants that I actually saw. I've printed only the successful child of each generation (i.e. the parent of the next generation) and one or two of its unsuccessful sisters. So, the picture basically shows just the one main line of evolution, guided by my aesthetic selection. All the stages in the main line are shown. Let's briefly go through the first few generations of the main line of evolution in Figure 4. The dot becomes a Y in generation 2. In the next two generations, the Y becomes larger. Then the branches become slightly curved, like a well-made catapult. In generation 7, the curve is accentuated, so that the two branches almost meet. The curved branches get bigger, and each acquires a couple of small appendages in generation 8. In generation 9 these appendages are lost again, and the stem of the catapult becomes longer. Generation 10 looks like a section through a flower; the curved side-branches resemble petals cupping a central appendage or 'stigma'. In generation 11, the same 'flower' shape has become bigger and slightly more complicated. I won't pursue the narrative. The picture speaks for itself, on through the 29 generations. Notice how each generation is just a little different from its parent and from its sisters. Since each is a little different from its parent, it is only to be expected that each will be slightly more different from its grandparents (and its grandchildren), and even more different still from its great grandparents (and great grandchildren). This is what cumulative evolution is all about, although, because of our high mutation rate, we have speeded it up here to unrealistic rates. Because of this. Figure 4 looks more like a pedigree of species than a pedigree of individuals, but the principle is the same. When I wrote the program, I never thought
that it would evolve anything more than a variety of tree-like shapes. I had
hoped for weeping willows, cedars of Lebanon,
|
|
The Blind Watchmaker eight legs like a spider, instead of six like an insect, but even so! I still cannot conceal from you my feeling of exultation as I first watched these exquisite creatures emerging before my eyes. I distinctly heard the triumphal opening chords of Also spiach Zaiathustia (the '2001 theme') in my mind. I couldn't eat, and that night 'my' insects' swarmed behind my eyelids as I tried to sleep. There are computer games on
the market in which the player has the illusion that he is wandering about in
an underground labyrinth, which has a definite if complex geography and in
which he encounters dragons, minotaurs or other mythic
adversaries. In these games the monsters are rather few in number. They are
all designed by a human programmer, and so is the geography of the labyrinth.
In the evolution game, whether the computer version or the real thing, the
player (or observer) obtains the same feeling of wandering metaphorically
through a labyrinth of branching passages, but the number of possible
pathways is all but infinite, and the monsters that one encounters are undesigned and unpredictable. On my wanderings through
the backwaters of We now have a much more realistic model of evolution than the monkeys typing Shakespeare gave us. But the biomorph model is still deficient. It shows us the power of cumulative selection to generate an almost endless variety of quasi-biological form, but it uses artificial selection, not natural selection. The human eye does the selecting. Could we dispense with the human eye, and make the computer itself do the selecting, on the basis of some biologically realistic criterion? This is more difficult than it may seem. It is worth spending a little time explaining why. It is trivially easy to select for a particular genetic formula, so long as you can read the genes of all the animals. But natural selection doesn't choose genes directly, it chooses the effects that genes have on bodies, technically called phenotypic effects. The human eye is good at choosing phenotypic effects, as is shown by the numerous breeds of
|
|
|
|
Accumulating small change 61
|
|
|
|
dogs, cattle and pigeons, and also, if I may say so, as is
shown by Figure It wouldn't be too difficult to make the computer select for vague general features like, say, tall-thinness, short-fatness, perhaps curvaceousness, spikiness, even rococo ornamentation. One method would be to program the computer to remember the kinds of qualities that humans have favoured in the past, and to exert continued selection of the same general kind in the future. But this isn't getting
|
|
62 The Blind Watchmaker us any closer to simulating natural selection. The important point is that nature doesn't need computing power in order to select, except in special cases like peahens choosing peacocks. In nature, the usual selecting agent is direct, stark and simple. It is the grim reaper. Of course, the reasons for survival are anything but simple - that is why natural selection can build up animals and plants of such formidable complexity. But there is something very crude and simple about death itself. And nonrandom death is all it takes to select phenotypes, and hence the genes that they contain, in nature. To simulate natural selection
in an interesting way in the computer, we should forget about rococo
ornamentation and all other visually defined qualities. We should concentrate,
instead, upon simulating nonrandom death. Biomorphs
should interact, in the computer, with a simulation of a hostile environment.
Something about their shape should determine whether or not they survive in
that environment. Ideally, the hostile environment should include other
evolving biomorphs: 'predators', 'prey',
'parasites', 'competitors'. The particular shape of a prey biomorph should determine its vulnerability to being
caught, for example, by particular shapes of predator biomorphs.
Such criteria of vulnerability should not be built in by the programmer. They
should emerge, in the same kind of way as the shapes
themselves emerge. Evolution in the computer would then really take off, for
the conditions would be met for a self-reinforcing 'arms race' (see Chapter If anybody is clever enough to do it, it
would be the programmers who develop those noisy and vulgar arcade games -
Space Invaders' derivatives. In these programs a counterfeit world is
simulated. It has a geography, often in three
dimensions, and it has a fast-moving time dimension. Entities zoom around in
simulated three-dimensional space, colliding with each other, shooting each
other down, swallowing each other amid revolting noises. So good can the
simulation be that the player handling the joystick receives a powerful
illusion that he himself is part of the counterfeit world. I imagine that the
summit of this kind of programming is achieved in the chambers used to train aeroplane and spacecraft pilots. But even these programs
are small-fry compared to the program that would have to be written to
simulate an emerging arms race between predators and prey, embedded in a
complete, counterfeit ecosystem. It certainly could be done,
|
|
Accumulating small change 63 Meanwhile, there is something else that is much easier, and which I intend trying when summer comes. I shall put the computer in a shady place in the garden. The screen can display in colour. I already have a version of the program which uses a few more 'genes' to control colour, in the same kind of way as the other nine genes control shape. I shall begin with any more-or-less compact and brightly coloured biomorph. The computer will simultaneously display a range of mutant progeny of the biomorph, differing from it in shape and/or colour pattern. I believe that bees, butterflies and other insects will visit the screen, and 'choose' by bumping into a particular spot on the screen. When a certain number of choices have been logged, the computer will wipe the screen clean, 'breed' from the preferred biomorph, and display the next generation of mutant progeny. I have high hopes that, over a large number of generations, the wild insects will actually cause the evolution, in the computer, of flowers. If they do, the computer flowers will have evolved under exactly the same selection pressure as caused real flowers to evolve in the wild. I am encouraged in my hope by the fact that insects frequently visit bright blobs of colour on women's dresses (and also by more systematic experiments that have been published). An alternative possibility, which I would find even more exciting, is that the wild insects might cause the evolution of insect-like shapes. The precedent for this - and hence the reason for hope - is that bees in the past caused the evolution of bee-orchids. Male bees, over many generations of cumulative orchid evolution, have built up the bee-like shape through trying to copulate with flowers, and hence carrying pollen. Imagine the 'bee-flower' of Figure 5 in colour. Wouldn't you fancy it if you were a bee? My main reason for pessimism is that insect vision works in a very different way from ours. Video-screens are designed for human eyes not bee eyes. This could easily mean that, although both we and bees see bee-orchids, in our very different ways, as bee-like, bees might not see video-screen images at all. Bees might see nothing but 625 scanning lines! Still, it is worth a try. By the time this book is published, I shall know the answer. There is a popular cliche, usually uttered in the tones Stephen Potter would have called 'plonking', which says that you cannot get out of computers any more than you put in. Other versions are that computers only do exactly what you tell them to, and that therefore computers are never creative. The cliche is true only in a crashingly trivial sense, the same sense in which Shakespeare never wrote anything except what his first schoolteacher taught him to write — words. I
|
|
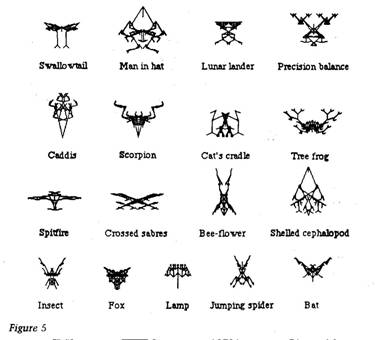
64 The Blind Watchmaker programmed EVOLUTION into the computer, but I did not plan 'my' insects, nor the scorpion, nor the spitfire, nor the lunar lander. I had not the slightest inkling that they would emerge, which is why 'emerge' is the right word. True, my eyes did the selecting that guided their evolution, but at every stage I was limited to a small clutch of progeny offered up by random mutation, and my selection 'strategy', such as it was, was opportunistic, capricious and short-term. I was not aiming for any distant target, and nor does natural selection. I can dramatize this by discussing the one time when I did try to aim for a distant target. First I must make a confession. You will have guessed it anyway. The evolutionary history of Figure 4 is a reconstruction. It was not the first time I had seen 'my' insects. When they originally emerged to the sound of trumpets, I had no means of recording their genes. There they were, sitting on the computer screen, and I couldn't get at them, couldn't decipher their genes. I delayed switching the computer off while I racked my brain trying to think of some way of saving them, but there was none. The genes were too deeply buried, just as they are in real life. I could print out pictures of the insects' bodies, but I had lost their genes. I immediately modified the program so that in future it would keep accessible records of genetic formulae, but it was too late. I had lost my insects. I set about trying to 'find' them again. They
had evolved once, so it seemed that it must be possible to evolve
them again. Like the lost chord, they haunted me. I wandered through You might think that it would
have been easy enough to reconstruct the evolutionary pathway, but it wasn't.
The reason, which I shall come back to, is the astronomical number of possible biomorphs that a sufficiently long evolutionary
pathway can offer, even when there are only nine genes varying. Several times
on my pilgrimage through
|
|
Accumulating small change 65 they were superficially 'convergent' (see next chapter), but it was good enough. This time there was no mistake: I wrote down the genetic formula, and now I can 'evolve' insects whenever I want. Yes I am piling on the drama a bit, but there is a serious point being made. The point of the story is that even though it was I that programmed the computer, telling it in great detail what to do, nevertheless I didn't plan the animals that evolved, and I was totally surprised by them when I first saw their precursors. So powerless was I to control the evolution that, even when I very much wanted to retrace a particular evolutionary pathway it proved all but impossible to do so. I don't believe I would ever have found my insects again if I hadn't had a printed picture of the complete set of their evolutionary precursors, and even then it was difficult and tedious. Does the powerlessness of the programmer to control or predict the course of evolution in the computer seem paradoxical? Does it mean that something mysterious, even mystical was going on inside the computer? Of course not. Nor is there anything mystical going on in the evolution of real animals and plants. We can use the computer model to resolve the paradox, and learn something about real evolution in the process. To anticipate, the basis of the resolution of
the paradox will turn out to be as follows. There is a definite set of biomorphs, each permanently sitting in its own unique
place in a mathematical space. It is permanently sitting there in the sense
that, if only you knew its genetic formula, you could instantly find it;
moreover, its neighbours in this special kind of
space are the biomorphs that differ from it by only
one gene. Now that I know the genetic formula of my insects, I can reproduce
them at will, and I can tell the computer to 'evolve' towards them from any
arbitrary starting point. When you first evolve a new creature by artificial
selection in the computer model, it feels like a creative process. So it is,
indeed. But what you are really doing is finding the
creature, for it is, in a mathematical sense, already sitting in its own
place in the genetic space of Some people fondly believe that chess-playing computers work by internally trying out all possible combinations of chess moves. They find this belief comforting when a computer beats them, but their belief is utterly false. There are far too many possible chess moves: the search-space is billions of times too large to allow blind stumbling to
|
|
66 The Blind Watchmaker succeed. The art of writing a good chess program is thinking of efficient short cuts through the search-space. Cumulative selection, whether artificial selection as in the computer model or natural selection out there in the real world, is an efficient searching procedure, and its consequences look very like creative intelligence. That, after all, is what William Paley's Argument from Design was all about. Technically, all that we are doing, when we play the computer biomorph game, is finding animals that, in a mathematical sense, are waiting to be found. What it feels like is a process of artistic creation. Searching a small space, with only a few entities in it, doesn't ordinarily feel like a creative process. A child's game of hunt the thimble doesn't feel creative. Turning things over at random and hoping to stumble on the sought object usually works when the space to be searched is small. As the search-space gets larger, more and more sophisticated searching procedures become necessary. Effective searching procedures become, when the search-space is sufficiently large, indistinguishable from true creativity. The computer biomorph
models make these points well, and they constitute an instructive bridge
between human creative processes, such as planning a winning strategy at
chess, and the evolutionary creativity of natural selection, the blind
watchmaker. To see this, we must develop the idea of The space we are talking about is genetic space. Each animal has its own position in genetic space. Near neighbours in genetic space are animals that differ from one another by only a single mutation. In Figure 3, the basic tree in the centre is surrounded by 8 of its 18 immediate neighbours in genetic space. The 18 neighbours of an animal are the 18 different kinds of children that it can give rise to, and the 18 different kinds of parent from which it could have come, given the rules of our computer model. At one remove, each animal has 324 (18 x 18, ignoring back-mutations for simplicity) neighbours, the set of its possible grandchildren, grandparents, aunts or nieces. At one remove again, each animal has 5,832 (18 x 18 x 18) neighbours, the set of possible great grandchildren, great grandparents, first cousins, etc.
|
|
Accumulating small change 67 What is the point of thinking in terms of
genetic space? Where does it get us? The answer is that it provides us with a
way to understand evolution as a gradual, cumulative process. In any one generation,
according to the rules of the computer model, it is possible to move only a
single step through genetic space. In 29 generations it isn't possible to
move farther than 29 steps, in genetic space, away from the starting
ancestor. Every evolutionary history consists of a particular pathway, or
trajectory, through genetic space. For instance, the evolutionary history
recorded in Figure 4 is a particular winding trajectory through genetic
space, connecting a dot to an insect, and passing through 28 intermediate
stages. It is this that I mean when I talk metaphorically about 'wandering'
through I wanted to try to represent this genetic space in the form of a picture. The trouble is, pictures are two-dimensional. The genetic space in which the biomorphs sit is not two-dimensional space. It isn't even three-dimensional space. It is nine-dimensional space! (The important thing to remember about mathematics is not to be frightened. It isn't as difficult as the mathematical priesthood sometimes pretends. Whenever I feel intimidated, I always remember Silvanus Thompson's dictum in Calculus Made Easy: 'What one fool can do, another can'.) If only we could draw in nine dimensions we could make each dimension correspond to one of the nine genes. The position of a particular animal, say the scorpion or the bat or the insect, is fixed in genetic space by the numerical value of its nine genes. Evolutionary change consists of a step by step walk through nine-dimensional space. The amount of genetic difference between one animal and another, and hence the time taken to evolve, and the difficulty of evolving from one to the other, is measured as the distance in ninedimensional space from one to the other. Alas, we can't draw in nine dimensions. I
sought a way of fudging it, of drawing a two-dimensional picture that
conveyed something of what it feels like to move from point to point in the
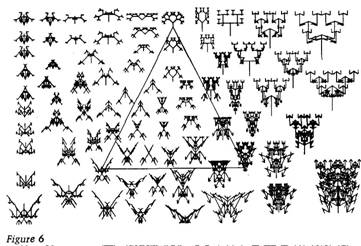
nine-dimensional genetic space of The triangle lies on a flat two-dimensional 'plane' that cuts through the nine-dimensional hypervolume (what one fool can do, another .
|
|
|
|
68 The Blind Watchmaker
|
|
|
|
can). The plane is like a flat piece of glass stuck through a jelly. On the glass is drawn the triangle, and also some of the biomorphs whose genetic formulae entitle them to sit on that particular flat plane. What is it that entitles them? This is where the three biomorphs at the corners of the triangle come in. They are called the anchor biomorphs. Remember that the whole idea of 'distance' in genetic 'space' is that genetically similar biomorphs are near neighbours, genetically different biomorphs are distant neighbours. On this particular plane, the distances are all calculated with reference to the three anchor biomorphs. For any given point on the sheet of glass, whether inside the triangle or outside it, the appropriate genetic formula for that point is calculated as a 'weighted average' of the genetic formulae of the three anchor biomorphs. You will already have guessed how the weighting is done. It is done by the distances on the page, more precisely the nearnesses, from the point in question to the three anchor biomorphs. So, the nearer you are to the insect on the plane, the more insect-like are the local biomorphs. As you move along the glass towards the tree, the 'insects' gradually become less insect-like and more tree-like. If you walk into the centre of the triangle the animals that you find there, for instance the spider with a Jewish seven-branched candelabra on its head, will be various 'genetic compromises' between the three anchor biomorphs. But this account gives altogether too much prominence to the three anchor biomorphs. Admittedly the computer did use them to calculate
|
|
|
|
Accumulating small change 69 the appropriate genetic formula for every point on the picture. But actually any three anchor points on the plane would have done the trick just as well, and would have given identical results. For this reason, in Figure 7 I haven't actually drawn the triangle. Figure 7 is exactly the same kind of picture as Figure 6. It just shows a different plane. The same insect is one of the three anchor points, this time the right-hand one. The other anchor points, in this case, are the spitfire and the bee-flower, both as seen in Figure 5. On this plane, too, you will notice that neighbouring biomorphs resemble each other more than distant biomorphs. The spitfire, for instance, is part of a squadron of similar aircraft, flying in formation. Because the insect is on both sheets of glass, you can think of the two sheets as passing, at an angle, through each other. Relative to Figure 6, the plane of Figure 7 is said to be 'rotated about' the insect.
|
|
|
|
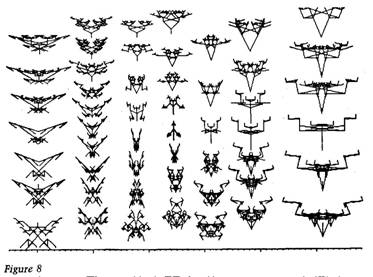
The elimination of the triangle is an improvement to our method, because it was a distraction. It gave undue prominence to three particular points in the plane. We still have one further improvement to make. In Figures 6 and 7, spatial distance represents genetic distance, but the scaling is all distorted. One inch upwards is not necessarily equivalent to one inch across. To remedy this, we must choose our three anchor biomorphs carefully, so that their genetic distances, one from the other, are all the same. Figure 8 does just this. Again the triangle is not actually drawn. The three anchors are the scorpion from Figure 5, the insect again (we have yet another 'rotation about' the
|
|
70 The Blind Watchmaker insect), and the rather nondescript biomorph at the top. These three biomorphs are all 30 mutations distant from each other. This means that it is equally easy to evolve from any one to any other one. In all three cases, a minimum of 30 genetic steps must be taken. The little blips along the lower margin of Figure 8 represent units of distance measured in genes. You can think of it as a genetic ruler. The ruler doesn't only work in the horizontal direction. You can tilt it in any direction, and measure the genetic distance, and hence the minimum evolution time, between any point on the plane and any other (annoy - ingly, that is not quite true on the page, because the computer's printer distorts proportions, but this effect is too trivial to make a fuss about, although it does mean that you will get slightly the wrong answer if you simply count blips on the scale).
|
|
|
|
These two-dimensional planes cutting through
nine-dimensional genetic space give some feeling for what it means to walk
through I said that the 'genetic ruler' of Figure 8 enables us to calculate the
|
|
Accumulating small change 71 minimum time it would take to evolve from one point to another. So it does, given the restrictions of the original model, but the emphasis is on the word minimum. Since the insect and the scorpion are 30 genetic units distant from one another, it takes only 30 generations to evolve from one to the other if you never take a wrong turning, if, that is, you know exactly what genetic formula you are heading towards, and how to steer towards it. In real-life evolution there is nothing that corresponds to steering towards some distant genetic target. Let's now use the biomorphs to return to the point made by the monkeys typing Hamlet, the importance of gradual, step-by-step change in evolution, as opposed to pure chance. Begin by relabelling the graticules along the bottom of Figure 8, but in different units. Instead of measuring distance as 'number of genes that have to change in evolution', we are going to measure distance as 'odds of happening to jump the distance, by sheer luck, in a single hop'. To think about this, we now have to relax one of the restrictions that I built into the computer game: we shall end by seeing why I built that restriction in in the first place. The restriction was that children were only 'allowed' to be one mutation distant from their parents. In other words, only one gene was allowed to mutate at a time, and that gene was allowed to change its 'value' only by +1 or -1. By relaxing the restriction, we are now allowing any number of genes to mutate simultaneously, and they can add any number, positive or negative, to their current value. Actually, that is too great a relaxation, since it allows genetic values to range from minus infinity to plus infinity. The point is adequately made if we restrict gene values to single figures, that is if we allow them to range from -9 to +9. So, within these wide limits, we are
theoretically allowing mutation, at a stroke, in a single generation, to change
any combination of the nine genes. Moreover, the value of each gene can
change any amount, so long as it doesn't stray into double figures. What does
this mean? It means that, theoretically, evolution can jump, in a single
generation, from any point in
|
|
72 The Blind Watchmaker are embarking on another of those astronomical calculations. There are nine genes, and each of them can take any of 19 values. So the total number of biomorphs that we could jump to in a single step is 19 times itself 9 times over: 19 to the power 9. This works out as about half a trillion biomorphs. Paltry compared with Asimov's 'haemoglobin number', but still what I would call a large number. If you started from the insect, and jumped like a demented flea half a trillion times, you could expect to arrive at the fox once. What is all this telling us about real evolution? Once again, it is ramming home the importance of gradual, step-by-step change. There have been evolutionists who have denied that gradualism of this kind is necessary in evolution. Our biomorph calculation shows us exactly one reason why gradual, step-by-step change is important. When I say that you can expect evolution to jump from the insect to one of its immediate neighbours, but not to jump from the insect directly to the fox or the scorpion, what I exactly mean is the following. If genuinely random jumps really occurred, then a jump from insect to scorpion would be perfectly possible. Indeed it would be just as probable as a jump from insect to one of its immediate neighbours. But it would also be just as probable as a jump to any other biomorph in the land. And there's the rub. For the number of biomorphs in the land is half a trillion, and if no one of them is any more probable as a destination than any other, the odds of jumping to any particular one are small enough to ignore. Notice that it doesn't help us
to assume that there is a powerful nonrandom 'selection pressure'. It
wouldn't matter if you'd been The tone of my previous paragraphs is open to a misunderstanding which I must dispel. It sounds, once again, as though evolution deals in distant targets, homing in on things like scorpions. As we have seen, it never does. But if we think of our target as anything that would improve survival chances, the argument still works. If an animal is a parent, it must be good enough to survive at least to adulthood. It is
|
|
|
|
Accumulating small change 73 possible that a mutant child of that parent might be even better at surviving. But if a child mutates in a big way, so that it has moved a long distance away from its parent in genetic space, what are the odds of its being better than its parent? The answer is that the odds against are very large indeed. And the reason is the one we have just seen with our biomorph model. If the mutational jump we are considering is a very large one, the number of possible destinations of that jump is astronomically large. And because, as we saw in Chapter 1, the number of different ways of being dead is so much greater than the number of different ways of being alive, the chances are very high that a big random jump in genetic space will end in death. Even a small random jump in genetic space is pretty likely to end in death. But the smaller the jump the less likely death is, and the more likely is it that the jump will result in improvement. We shall return to this theme in a later chapter. That is as far as I want to go in drawing
morals from Sitting somewhere in this huge mathematical space are humans and hyenas, amoebas and aardvarks, flatworms and squids, dodos and dinosaurs. In theory, if we were skilled enough at genetic engineering, we could move from any point in animal space to any other point. From any starting point we could move through the maze in such a way as to recreate the dodo, the tyrannosaur and trilobites. If only we knew which genes to tinker with, which bits of chromosome to duplicate, invert or delete. I doubt if we shall ever know enough to do it, but these dear dead creatures are lurking there forever in their private corners of that huge genetic hypervolume, waiting to be found if we but had the knowledge to navigate the right course through the maze. We might even be able to evolve an exact reconstruction of a
|
|
74 The Blind Watchmaker dodo by selectively breeding pigeons, though we'd have to live a million years in order to complete the experiment. But when we are prevented from making a journey in reality, the imagination is not a bad substitute. For those, like me, who are not mathematicians, the computer can be a powerful friend to the imagination. Like mathematics, it doesn't only stretch the imagination. It also disciplines and controls it.
|