Selections from Julia E. Diggins, String, Straightedge, and Shadow Viking Press, New York , 1965. (Illustrations by Corydon Bell)

13. "DICE OF THE GODS"

As time went on, the Pythagoreans made even more exciting Discoveries-and gave them strange cosmic meanings.

This curious blend was characteristic of Pythagorean geometry. For the initiates of the Brotherhood were seeking a special key to the universe in this wonderful new realm of numbers and abstract forms: triangles, circles, squares, spheres, and the more elaborate forms they made themselves.

And their search had a thrilling climax. After long and painstaking experiments, they discovered the five regular solids. These were remarkable and beautiful polyhedra, or shapes with many faces.

The full tale of these five solids can only be guessed at from

106

bits of legend and history, for all the experiments were top secrets, of course.

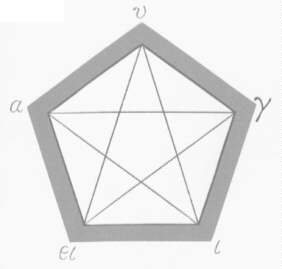
To impress this on newcomers, perhaps the first thing they were shown was how to make a mystic "pentagram," the emblem that members of the Order wore on their clothing. By means of a secret device (which we will explain later) a five-sided figure, or pentagon, was traced on cloth. Then its points were connected with diagonals to make a five-pointed star. Finally, around the five points of the star were placed the letters of the

Greek word for health, (hygeia), from which we get the word "hygiene."

This was the sacred symbol of the Pythagorean Order-the magic pentacle" that remained a favorite device of sorcerers and conjurors for many centuries. But it was also an experimental discovery: the first known use of letters on a geometric figure.

107
Possibly the next experiment shared with newcomers was a basic one with tiles. Ordinary floor tiles had yielded the easiest example of the Pythagorean theorem. So the Secret Brotherhood went on with a painstaking study of these close-fitting forms that covered many Greek floors.

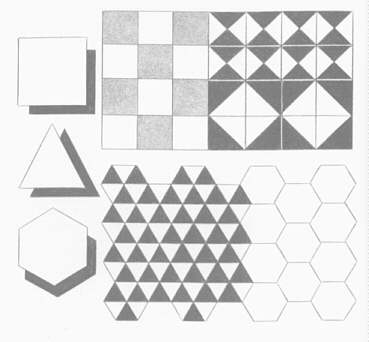
They made loose tiles of various shapes and placed them in

patterns on the ground. And they reached a striking conclusion. There were only three regular shapes of tiles that would fit together perfectly to cover a flat area completely: triangles (three sides), squares (four sides), hexagons (six sides).

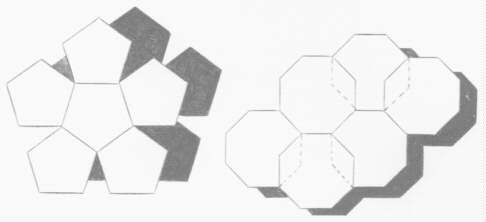
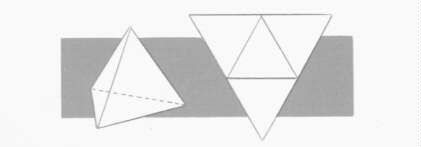
If they tried pentagons, they got a beautiful blossom like design, but there were gaps between the tiles, and tiles of more than six sides would always overlap. No other regular geometric forms of the same size and shape could be so combined.

They explained this mystery to the newcomers: "Since there are four right angles (360 ) around a point, you can only use forms whose corner angles together will make that total. There are just three possibilities: six equilateral triangles with 60 angles, four squares with 90 angles, and three hexagons with 120 angles."

From this simple experiment came the fascinating idea of making "solid angles" by fastening tiles together with mortar, or gluing together shapes of wood, or sewing together pieces of leather. And this led to building shapes with the solid angles.

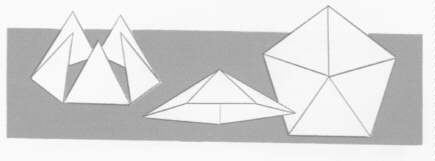
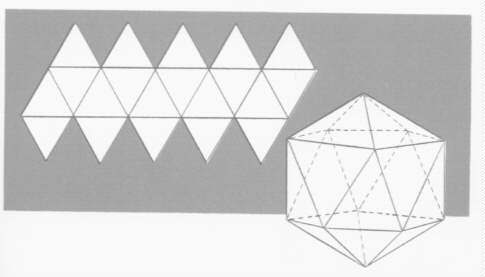
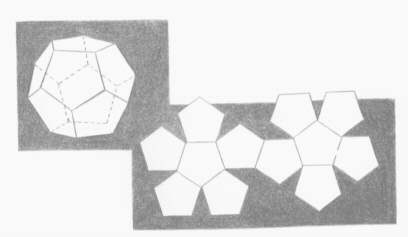
They called them regular solids because all the edges and faces and angles in each solid were equal. And after much experimenting, as we have said, they found five of these solids. The first two had been known from the most ancient times, but the next two were shapes that men had never seen before. As for the fifth, it was such a startling discovery that they thought they had upset the order of the universe!

109

The Cube. They mortared three square tiles into an angle, and fitted on three more tiles to form a cube with six square faces, which they called a hexahedron.

The Regular Pyramid. They put together three equilateral triangles into a solid angle, then added one more, to make the base of their four-faced tetrahedron.

The Octahedron. This was made with two solid angles of four equilateral triangles each, so they gave this eight-faced figure the name octahedron.

The Icosahedron. Here was a real challenge. When they put together five equilateral triangles, they got a surprise. The open base of this solid angle was a pentagon. Now they could trace one perfectly for their emblem, instead of just drawing it freehand. (Of course, the device was kept secret.) But how could they make a regular solid, with five equilateral triangles around each vertex? All their early attempts were failures. Finally, someone got the right inspiration-five equilateral triangles for the top, and five triangles for the bottom, and then a center band of ten more triangles based on the old Babylonian pattern. They had made an icosahedron with twenty triangular faces.

The Dodecahedron. This last form was made with the pentagons so dear to the Pythagorean Order. They used that flowerlike pattern of a single pentagon surrounded by five others-the tiles that would not fit together on the flat floor. But if the sur- rounding ones were lifted up, then all six pentagons fitted per-fectly in a solid cuplike shape. This could be capped by an inverted one just like it to yield the most difficult and beautiful of the five regular solids: the dodecahedron with its twelve pentagonal faces.

These five shapes created a great stir among the first geometers who studied them. Men examined them in fascination and awe, handling them, turning them around in different positions, look-ing through them as if they were glass. And it was inevitable that the Pythagoreans should finally give them mystical meanings.

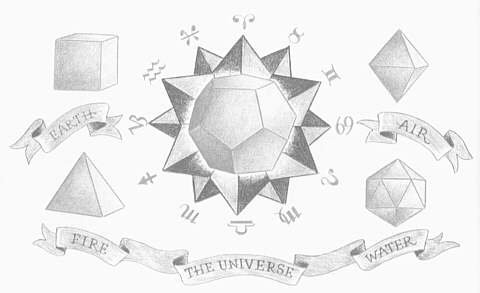
By that time the Secret Brotherhood had spread to many towns and islands of Sicily and southern Italy. The Sicilian members were friendly with another strange teacher who lived near Mount Etna, Empedocles, who dressed all in purple, gave away his money, and did scientific experiments Empedocles taught that the world was made of earth, air, fire, and water, and the first four regular solids came to be identified with these "elements. We know the identification from a famous passage in one of Plato's Dialogues, where it is made by a Pythagorean from Locri in time south of Italy. About the fifth solid, there were many weird stories. Its existence was kept secret as it seemed to require a fifth "element."

The esoteric reasoning g, as repeated later, went something like this:

"The cube, standing firmly on its base, corresponds to the stable earth. The octahedron, which rotates freely when held by its two opposite corners, corresponds to the mobile air.

"Since the regular pyramid has the smallest volume for its surface, and the almost spherical icosahedron the largest, and these are the qualities of dryness and wetness, the pyramid stands for fire amid the icosahedron for water."

As for the last-found regular solid, with its twelve faces, "Why not let the dodecahedron represent the whole universe, since the Zodiac has twelve signs!"

Such notions were typical of that age. And more than two thousand years later, the famous astronomer Kepler was still so awed by the unique properties of the five regular solids that he tried to apply them as planetary orbits: he assigned the cube to Sattmrn, the pyramid to Jupiter, the dodecahedron to Mars, the icosahedron to Venus, and the octahedron to Mercury, and he

designed a machine to show this! Of course, the attempt was a failure.

Yet even today, these solids seem almost magical in their beauty and their interrelations.

In the first place, it is quite startling that there are only five. An infinite number of regular polygons can be inscribed in a circle-their sides becoming so small that they approach the form of the circle itself. But it is not so with regular convex polyhedra inscribed in a sphere. There are only these five possible shapes, and no others.

And these five shapes are connected with one another in a most remarkable way. All five can be fitted together, one inside the next, like the compartments of some magic box. And they are further linked by a strange inner harmony. They can be inscribed in themselves or each other, in certain endless rhythmic alternations. So it's no wonder the five regular solids were long referred to as the "dice of the gods."